语法分析基础

编译的第一步是词法分析，第二步是语法分析。词法分析产生的结果是标识符，第二步是判断源程序文法是否合法。例如if{...}就是不合法的文法，但是他产生的标识符都是正确的。

工作原理：通过上下文无关文法产生的文法式，识别输入字符串是否是一个句子。从左至右每次读入一个字符进行规则匹配。

问题及解决

左递归

例如

规则为P->Pa
字符串为a
起始非终结符为P
读入a后将栈中的P展开为Pa,然后因为是从左往右匹配因此读入P，展开为Paa,如此递归，得到死循环

消除递归的方法：

消除直接左递归

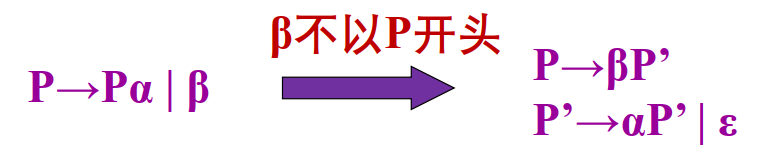
经过这样的转换之后产生的语言没有改变，但是消除了直接的左递归

再将它一般化得：

$\begin{aligned} A &\to A \alpha_1 | A\alpha_2 | \dots | A \alpha_m | \beta_1 | \beta_2 | \dots | \beta_n\\ 则可以改写为\\ A &\to \beta_1 A^{'} | \beta_2 A^{'} | \dots | \beta_n A^{'}\\ A &\to \alpha_1 A^{'} | \alpha_2 A^{'} | \dots | \alpha_m A^{'} | \varepsilon \end{aligned}$

通过上面的方法消除了直接左递归，但是还可能经过若干次转换之后又形成了左递归，例如

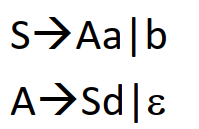
将A代入就形成了左递归

消除左递归的一般算法：

条件：不含回路(P=>P),不含以$\varepsilon$为右部的产生式

将文法中所有规则按任意一种顺序排列成$P_1 , P_2 , P_3 …$按此顺序执行

for i=1 to n do
    for k=1 to i-1 do //i-1而不是n
        将Pi中包含Pk的规则全部代入
        消除Pi中的左递归

化简前面得到的文法，去除那些由起始符号永远无法到达的非终结符产生的规则

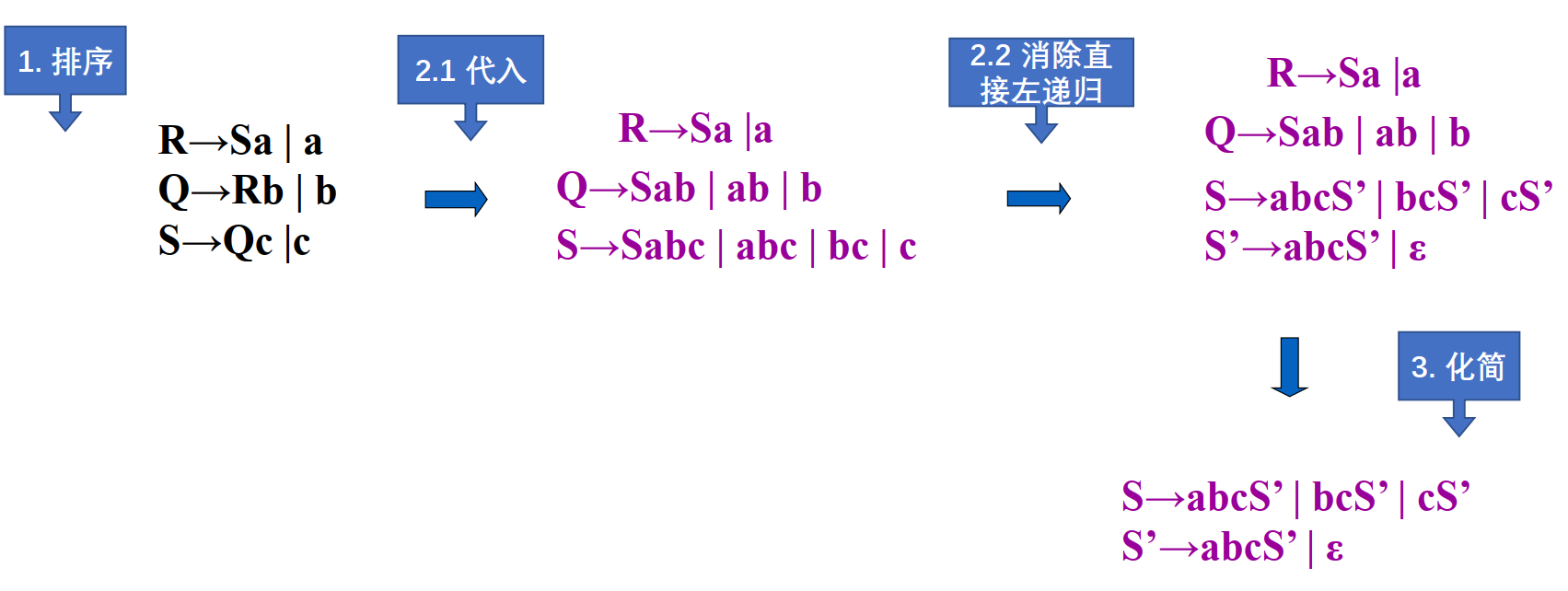
代入时Q代入的是经过第一次循环产生的R而不是最开始的R。化简时将从S无法到达的规则删除

回溯

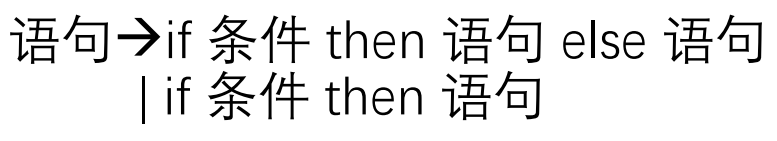
如上图，如果此时读入i可以同时进入两个状态，需要读入更多的字符才可以判断具体是哪个状态，这样需要占据大量资源并且容易导致程序错误。

解决方法：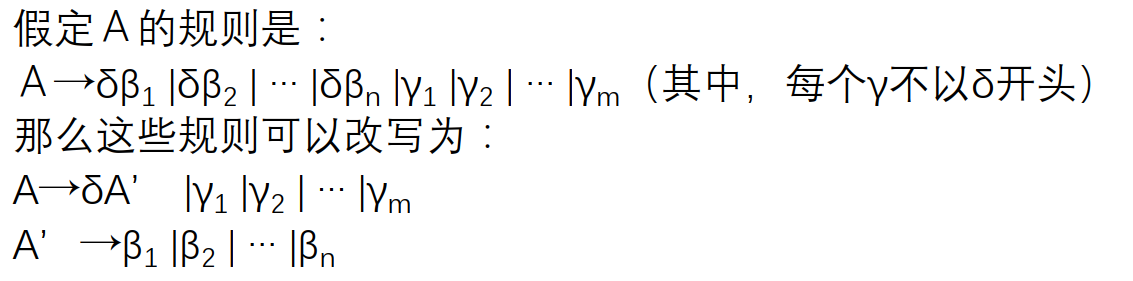

其中$\delta$是这些规则中相同的部分

通过反复提取左因子，我们可以将所有非终结符的所有First集变为两两不相交，但是回引入大量的新字符.

First($\alpha$)是所有$\alpha$推导的可能的开头终结符或$\varepsilon$

如果A->$\alpha_1 | \alpha_2 | …$, 且First($alpha_i ) \cap First(\alpha_j ) = \oslash$，则我们可以唯一的将字符推给某个模式，这样就无需回溯。

LL(1)

LL(1)标识从左向右推导，每次只看一个字符。

要构造不带回溯的自顶向下分析的文法(LL(1)文法)条件：

文法不含左递归(验证方法为使用消除左递归算法运行一遍，如果和原来相比没有变化则不含左递归）
每一个非终结符的各个产生式的First集两两不想交，即A->$\alpha_1 | \alpha_2 | …$, First($alpha_i ) \cap First(\alpha_j ) = \oslash$
对于每个非终结符A，若它的First包含$\varepsilon$,则First(A) $\cap$ Follow(A) = $\oslash$

使用LL(1)进行匹配的模式为：

如果要使用非终结符A进行匹配，输入符号为a，A的所有产生式为$\alpha_1 | \alpha_2 | …$
若a $\in First(\alpha_i )$,则将$\alpha_i$压入栈中进行下一步分析
如果没有任何一个First匹配成功，但是存在$\varepsilon$，则使用Follow(A)进行判断，如果Follow(A)中有a，则将A弹出栈(将A弹出然后再将$\varepsilon$压入)
如果都没匹配上，这说明有语法错误

构造First集算法

应用如下规则，直到First不再增大为止：

如果X$\in V_T$(终结符集合)，则First(X) = {X}
如果$X \in V_N$(非终结符集合),且有产生式X->a…,则将a假如First(X)中，如果X->$\varepsilon$也是一个产生式，则将$\varepsilon$加入First(X)中
如果X->$Y_1 Y_2 … Y_N$,首先将First($Y_1$) - {$\varepsilon$}添加进First(x),如果First($Y_1$)中包含$\varepsilon$，则将First($Y_2$) - {$\varepsilon$)添加进First(X)中。依次类推，如果推导最后First($Y_N$)也包含$\varepsilon$，则将$\varepsilon$添加进$First(X)$中

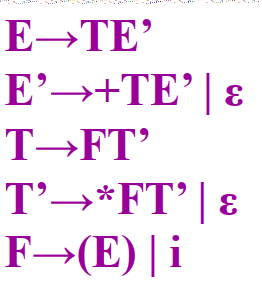
构造Follow集算法

Follow是非终结符后随的终结符号的集合

构造规则：

对于开始符号S，将#(结束符)添加到Follow(S)中
若A->aB$\beta$是一个产生式($\beta$可以是终结符也可以是非终结符),将First($\beta$) - {$\varepsilon$)添加到Follow(B)中
若A->$\alpha$B是一个产生式，或A->$\alpha$B$\beta$而$\varepsilon \in First(\beta$),则将Follow(A)添加到Follow(B)中

对于第二条规则很好理解，如果B后面是一个终结符，那么符合定义。如果是非终结符，那么First(A)就是第一个符号。而对于第二个则是由于它是这个式子中的最后一个字符，因此B的Follow集就是A的Follow集

例如$E^{‘}$的Follow集由于第一条，因此包含Follow(E)

分析表的构造方法

分析表就是将根据First集和Follow集构造一张表判断读入当前字符后下一个状态是什么。

构造方法：

对于每个A->$\alpha$(如A->Ba, A->c可以，A->Bc | a不能，它属于两条规则)执行如下步骤
- 对于每个a $\in First(\alpha$),将A->$\alpha$填入M[A, a]位置
  - 若$\varepsilon \in First(\alpha )$，则对于任何b $\in Follow(A)$,将$A->\varepsilon$填入M[A, b]中
  - 对于所有无定义的M[A, a]标上出错标志

例：